Recently I learned about the existence of what is known as Google
Foobar also known as “Google secret recruiting
program” or “How much bunnies can you rescue before wanting to kill someone” and
being the stubborn me that I am, I decided to force my way in and try the
challenges!
…
I didn’t expected to be able to get in but it seems I did, so I guess I’m
indebted to do a writeup or something? Oh well, I won’t cry over easy and
interesting content for my blog.
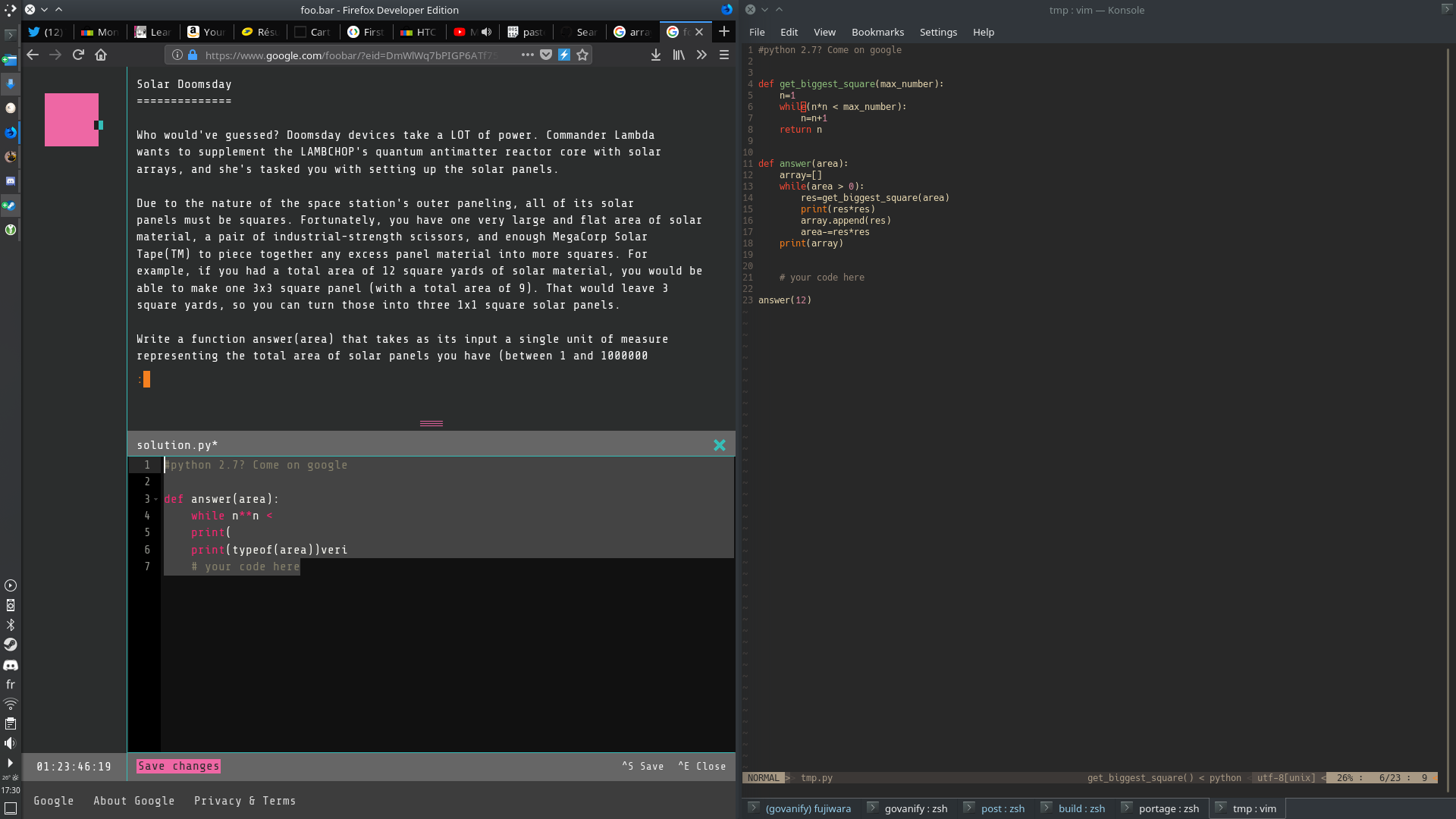
This is Google Foobar
So as you can see, Foobar is basically a website which contains a unix-like
shell, based on “jQuery Terminal”, which does have some standard unix commands,
including some which aren’t listed in the help command, namely mount or
cat.
When you can finally access foobar they’re prompting you to use the help command
to see the standard set of commands one would use, and to use the command
request whenever you’re ready, sending a POST request to
https://foobar.withgoogle.com/api/v1/commands/request/ and adding a folder
into your home directory(https://foobar.withgoogle.com/api/v1/files/).
This folder always contains 4 files: solution.py,
solution.java, constraints.txt and readme.txt which you can read using the
less command(listed in help) or cat(not listed but super handy to copy stuff,
since i never got less to honour linefeeds for some reason).
The solution files are supposed to contain, well, your solutions, constraints
tells you the stuff like “python 2.7 only basic libs” and readme the problem.
You always have to write a function answer which answers (how surprising) the
problem, either in java or in python. Foobar tests those by using a test VM
which, in the case of python, is isolated by nsjail and interacts with the file
descriptor 3 outside of the VM since it virtually have no other access to
outside data, but more onto that much later. They test it to up to 10 test
cases(can be as low as 5 though, ie the combinatorics problem I’m talking about
below, and you can then submit your problem to be able to request a new one et
cetera. A little thing to note is that, however, all those challenges are
timed(the first being 2days and the last being 22 iirc) and that once you
submitted a challenge it is removed from your home folder. For this reason
I’d like to thank very much the creator of UNIX to have put timestamps in files,
so that I know which challenges I did in which order, all hail ls -latr!
Foobar is also organized per “levels”, which contains a different number of
challenges each time, my session had 1 for level 2, 2 for level 2, 3 for level
3, four 2 for level 4 and 1 for level 5, all of which are organized in a
chronological order below.
But all this talk is boring for those interested in actual problems so I’ll zap
over the intelligence I gathered and begin on the actual challenges!
Solar Doomsday
Before talking about the challenges directly I’d like to note that my codestyle habits evolved when doing those challenges because of a. one reason I’ll explain at the bottom and b. I went to “aww those challenges are easy” to “how was I even supposed to think about this??”, but enough with my rants, let’s get it on with the first challenge.
This problem is pretty easy(and hopefully, knowing it is the first one): they ask you to decompose a number in squares and only put the largest squares you can in it. Solving it is pretty simple too: you get the biggest square that doesn’t overflow your number, you remove the square from the number, repeat, nothing really hard there.
def get_biggest_square(max_number):
n=1
while(n*n < max_number+1):
n=n+1
return n-1
def answer(area):
if(area > 1000000 or area < 1):
raise ValueError('Area is outside of bounds')
array=[]
while(area != 0):
res=get_biggest_square(area)
array.append(res*res)
area-=res*res
return arrayOh yeah, last thing before we move on: Those versions are uncommented versions of the algorithms because this article is way too large already, I’ll add a git repository at the end which keeps them as is to when I submitted them. Also sorry for making you miss the fun of the original questions but not only did I not saved them but this article would be huge if I had to embded them into it, so if one problem interests you, look it up!
Ion Flux Relabelling
This one is pretty annoying to explain without technical talks about trees so here, take this from the original probmlem question I looked up online because I saved none of them!
7
3 6
1 2 4 5
Write a function answer(h, q) - where h is the height of the perfect tree of
converters and q is a list of positive integers representing different flux
converters - which returns a list of integers p where each element in p is the
label of the converter that sits on top of the respective converter in q, or -1
if there is no such converter. For example, answer(3, [1, 4, 7]) would return
the converters above the converters at indexes 1, 4, and 7 in a perfect binary
tree of height 3, which is [3, 6, -1].
Now that the problem make(at least some) sense I can say that this problem wasn’t much harder than the last one but used some basics of CS theory, trees in that case, but could totally be solved without its knowledge. In this case we get the biggest element that can find a top(ie top-1) and if our number is between this and 0 it will have a number above it. We then do a recursive check; if the item is equal or inferior to the top of the left node then it is in the left node, otherwise proceed with the right with the same logic until we find the number as either the left node or right node, making it on top of those.
def find_item(item,cur,dif):
right_node=cur-1
left_node=right_node-dif//2
if(right_node==item or left_node==item):
return cur
else:
if(item<=left_node):
return find_item(item,left_node,dif//2)
else:
return find_item(item,right_node,dif//2)
def answer(h, q):
if(h > 30 or h < 1):
raise ValueError('Height is outside of bounds')
if(len(q) > 10000 or len(q) < 1):
raise ValueError('Flux converters list is outside of bounds')
items=(2**h)-1
array=[]
for i in range(len(q)):
if (q[i]<items and q[i]>0):
array.append(find_item(q[i],items,items-1))
else:
array.append(-1)
return array En Route Salute
I’d say this one was easier than the last one when you figured out how to do it, as it required no real formal knowledge, but problems at this point are still pretty easy anyways so classifying them by difficulty makes little sense. In this case we were given a string containing <, > or - and we had to know the number of arrows that crossed, knowing that they all move one step at a time. To figure this out you just had to save the position of each arrow and figure out their distance: if a right arrow was on the left of a left arrow then they’ll obviously cross.
def answer(s):
if(len(s) > 100 or len(s) < 1):
raise ValueError('Height is outside of bounds')
s = list(s.replace("-",""))
left = []
right = []
res=0
for i in range(0,len(s)):
if s[i] == '<':
left.append(i)
if s[i] == '>':
right.append(i)
for i in right:
for y in left:
if i < y:
res+=1
for i in left:
for y in right:
if y < i:
res+=1
return res Fuel Injection Perfection
And the easy part stops here, this is where Foobar becomes really tricky and
focus on what it likes most: tricky math questions! Unfortunately it seems more
than a few share of people got this challenge and I ended up having the solution
almost handed out to me when looking at stackoverflow(when someone tells you
they’re working on a “challenge” and the reduced test case looks about the same
there isn’t much doubt about it…). For some context you can do fairly easily
the \(n^2\) way but the time limit is not really helping our case there.
I also removed my asserts from this point forward for a reason I’ll explain at
the bottom of this article.
It was still quite fun to understand though!
The problem is that given a number, and given 3 operations: add, remove, or
divide per 2 only if the number is even, you have to find the quickest way to
reduce this number to 1.
If you can divide per 2, the answer is obvious: you do because that’s the
fastest way to cut down the number, but then the finicky part is: should you add or remove to the
number to get to the result ASAP? Ie you can do 3->4->2->1 or you can do
3->4->1, and the time limit doesn’t allow us to try both for each given number.
The answer to that happens to lie in binary: we calculate how to get the maximum
of 000 in the rightmost bits, which in turn make us prefer to add when we are in
a situation where we have 111, making us push to 000 and making the division per
2 easier.
Kind of a letdown to get spoiled but eh, we’re getting in the territory of the
“if you don’t know that you’re screwed”.
def answer(n):
n=int(n)
res = 0
while(n!=1):
if(n%2==0):
n=n/2
elif((n==3) or ((n+1)&n) > ((n-1)&(n-2))):
n-=1
else:
n+=1
res+=1
return resQueue To Do
Remember the problem before that one? Look up “XOR Reduction” and you have the same result for this one! This problem was about XORing reduction, as you could do it easily without the time/memory limit. See the cube of numbers below?
0 1 2 /
3 4 / 5
6 / 7 8
Great, so this is a cube starting by 0, length of 3, the / are included to help with the problem. The point is to XOR all the numbers on the left side of the slash aka 0^1^2^3^4^6. The basic idea is to just xor everything in a loop and reduce by one each time the numbers to XOR, but for huge cubes this can take a long time and thus we had to figure out some XOR reduction for long lists like that. I tried my best to figure it out by myself but then again you can find plenty of XOR reduction resources on the net, so believe me as you wish I guess. For the theory basically XOR repeats itself when XORing lists of following numbers(the thing we’re trying to reduce), so we can reduce a ton of XOR operations into an \(O(1)\) one, helping a lot, given a rotation noted below, differing for even and odd numbers.
def xor(a, b):
if(a%2==0):
xor_rotation = [b, 1, b+1, 0]
else:
xor_rotation= [a, a^b, a-1, (a-1)^b]
return xor_rotation[(b-a)%4]
def answer(start, length):
res=0
for i in range(0, length):
res ^= xor(start+(length*i), start+(length*i)+(length-i)-1)
return resFind the access code
Look up “lucky triples” on stackoverflow, first result. I’m not even kidding. With that even the people trying to figure it out themselves would cheat without wanting to, aaaaaaaaaargh. Either way the goal was to find lucky triples in a list, basically one number that divides another in a small-to-big order. Solving that even without looking it up is trivial though, you see if two numbers divide themselves, then you see if this other number divides another and boom you solved it.
def answer(l):
triples = 0
pairs = [0]*len(l)
for i in range(1, len(l)-1):
for j in range(i):
if(l[i]%l[j]==0):
pairs[i]+=1
for i in range(2, len(l)):
for j in range(1, i):
if(l[i]%l[j]==0):
triples += pairs[j]
return triples Distract the Guards
Ok so take back all I said about level 3 challenges and the copypasta fest it was, we are entering level 4, where challenges finally get interesting. I mean guard betting bananas on thumb wrestling kind of way, but still! Well then the problem is that we have a list of bananas, and we know guards pairing up in banana fights
- always bets the amount of the guy who have less bananas
- the guy who have less bananas always win.
There is a catch though, when both gets an equal number of bananas they stop
thumb wrestling. And we don’t want that. Because we want them to keep being busy
or something, guess their peripheral vision isn’t quite as developped as animals
yet.
Anyways the first part of the problem is about combinatorics maths: knowing when
the guard loops:
Let \(k\) be the largest positive integer such that \(a > (2^k - 1)b\).
If \(a = b(2^k - 2^{m-1} - 1)\) or \(a = b(2^{k+1} - 2^m - 1)\) then we are in
an infinite loop. We can deduce from that that if \(a+b\) is a power of two,
for \(a+b\) being divided by their common divisor, then we are in a loop.
The second part is quite easy actually: you want to pair up the maximal amount
in an infinite loop, so you find the infinite loops, pair the
lowest-numbers-of-infinite-loop guard to the next-lowest-numbers-of-infinite-loop
and you can find the maximum amount that can be paired!
While the problem looks quite easy explained like that(I mean excepted the
maths) I still began to switch to pen and paper from that point forward, as it
was getting pretty theoric.
from fractions import gcd
def loops(x, y):
res = (x+y)/gcd(x,y)
return bool(res & (res - 1))
def remove(guards, ref):
for i in range(len(guards)):
j = 0
while j < len(guards[i]):
if(guards[i][j]==ref):
guards[i].pop(j)
j+=1
guards[ref]=[-1]
def answer(banana_list):
guards= [[] for i in range(len(banana_list))]
bad=0
for i in range(len(guards)):
for j in range(len(guards)):
if(loops(banana_list[i], banana_list[j])):
guards[i].append(j)
to_process=len(banana_list)
while(to_process>0):
min_num=0
for i in range(len(guards)):
if(i!=0 and (len(guards[i])<len(guards[min_num]) or guards[min_num]
== [-1]) and guards[i]!=[-1]):
min_num=i
if((len(guards[min_num])) == 0 or (len(guards[min_num])==1 and
guards[min_num][0] == guards[min_num]) and guards[min_num] !=
[-1]):
remove(guards, min_num)
to_process-=1
bad+=1
else:
min_node=guards[min_num][0]
for i in range(len(guards[min_num])):
if(i!=0 and guards[min_num][i]!=min_num and len(guards[guards[min_num][i]])<len(guards[min_node])):
min_node=guards[min_num][i]
if(guards[min_node]!=[-1]):
remove(guards, min_num)
remove(guards, min_node)
to_process-=2
return bad Bringing a Gun to a Guard Fight
THIS ONE WAS WILD. SERIOUSLY. It have to be the one problem a raytracing engineer faced one day in his life and never forgot. Gosh it took me so much time to figure this one out, easily the hardest for me in this whole set of challenges. Basically you are in a room of given dimension and can shoot a laser beam that reflects on walls and you need to figure out exactly in which directions you can shoot so that it gets to your ennemy, given a max distance and your position. For that one problem I made a huge essay on how it works in the comments which I’m going to post below:
The first thing you had to realize in order to solve this challenge is that you
could simply mirror the room and check if the beam gets where you want. Let me
show you:
In our case let us make a room of dimension [3,2], with the position of the
target at [1,2]. For the sake of simplicity let us imagine the beam is shot at
[1,2] and so we are trying to shot ourselves. We get something like this:
-----
|*xx|
|xxx|
-----
If we shoot with a vector of [1,0], aka straight ahead, we will get this result:
-----
|*~~|
|xxx|
-----
We can see that the beam gets back to you directly, thanks to the reflection,
and that the goal is achieved! But there is another way to do that:
----- -----
|*~~| |~~*|
|xxx| |xxx|
----- -----
We can here realize that, by putting a mirror version of the room where the beam
gets, we can make a straight line instead of calculating the reflection and see
that it gets to our original target, [1,2], being ourselves!
The good thing with that is that it also allows us to determine the distance
needed by the beam to get through, and thus we can mirror the rooms up to the
maximum distance easily.
The next thing to realize was that room mirrors in a pattern, see the below
diagram:
-----
|*xx|
|xxx|
-----
[...] ----- [...]
|xxx|
|*xx|
-----
----- ----- ----- ----- -----
|*xx| |xx*| |*xx| |xx*| |*xx|
|xxx| |xxx| |xxx| |xxx| |xxx|
----- ----- ----- ----- -----
-----
|xxx|
|*xx|
-----
[...] ----- [...]
|*xx|
|xxx|
-----
x always repeats in the same way, and so does y
Thus we need to figure out how to calculate how to mirror one room twice and we
can make an entire atlas of mirrored rooms!
In our case though the function below only calculates the mirrors of the point
of coordinates node across an atlas of length (distance*2)^2
Sooo the hard part about this was figuring out about the mirroring of the room. I was talking with a friend and when I told him about a specific thing that the problem stated on the rooms, that if you shoot in the corner it reflects perfectly we both had an Eureka moment: “Wait, isn’t the room reflection symmetric to itself?” and then I looked up some 2D plane mirroring(which leaded to a ton of maths I didn’t need actually and so I had to figure out a 1D transform on my own) and then just verify the angles and ensure the distance of the guard is before yourself.
def mirror_atlas(node, dimensions, distance):
node_mirrored=[]
for i in range(len(node)):
points=[]
for j in range(-(distance//dimensions[i])-1, (distance//dimensions[i]+2)):
points.append(get_mirror(j, node[i], dimensions[i]))
node_mirrored.append(points)
return node_mirrored
def get_mirror(mirror, coordinates, dimensions):
res=coordinates
mirror_rotation=[2*coordinates, 2*(dimensions-coordinates)]
if(mirror<0):
for i in range(mirror, 0):
res-=mirror_rotation[(i+1)%2]
else:
for i in range(mirror, 0, -1):
res+=mirror_rotation[i%2]
return res
def answer(dimensions, your_position, guard_position, distance):
mirrored = [mirror_atlas(your_position, dimensions,
distance),mirror_atlas(guard_position, dimensions, distance)]
res=set()
angles_dist={}
for i in range(0, len(mirrored)):
for j in mirrored[i][0]:
for k in mirrored[i][1]:
beam=atan2((your_position[1]-k), (your_position[0]-j))
l=sqrt((your_position[0]-j)**2 + (your_position[1]-k)**2)
if [j,k] != your_position and distance >= l:
if((beam in angles_dist and angles_dist[beam] > l) or beam not in angles_dist):
if i == 0:
angles_dist[beam] = l
else:
angles_dist[beam] = l
res.add(beam)
return len(res) Expanding Nebula
Clearly the second hardest problem of this set, right after the banana thumb
wrestling one.
You were given a 2D grid(matrix) of booleans and needed to figure out the number of
possible permutations before it, knowing that a boolean is true if it had only
one true neighbor(including itself, right, bottom and bottom right) and false otherwise.
Since some cells cannot be calculated the grid loses one dimension in both axis
at each step.
The hard part of this is akin to the XOR Reduction problem, again: how the hell
do we not go over the time limit?? For this we just setup an index for each cell
of coordinates a,b given the last row + current move history to figure out if we
already had a similar situation to avoid recursion, not really complicated but
way harder to figure out than it looks(thanks Internet for that one).
def answer(state, a=0, b=0, past=0, solutions=0, history=0):
if(past==0):
past=[[True] * (len(state[0])+1) for i in range(len(state)+1)]
solutions = {}
history = []
if(b==len(state[0])+1):
return True
res=0
index=((a,b), tuple(history[-(len(state)+2):]))
if index in solutions:
return solutions[index]
for cell in [True, False]:
if (not a or not b) or len(set([((past[a][b-1] + past[a-1][b]
+ past[a-1][b-1] + cell)==1), state[a-1][b-1]]))==1:
history.append(cell)
past[a][b] = cell
res+=answer(state, a=(a+1)%(len(state)+1),
b=b+(a+1)//(len(state)+1), past=past,
solutions=solutions, history=history)
history.pop()
solutions[index]=res
return resEnd and hack stuff
Here we are, we finished all the challenges, we can use recruitme whenever to
spam employers with our wits, and we even have a nice cipher to end this game
on!
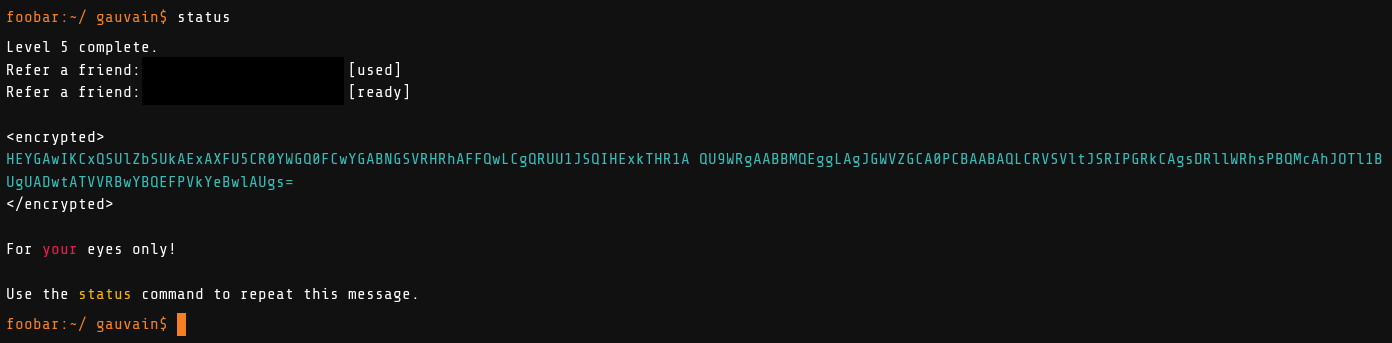
Awww, even thinking of greeting me in the encrypted end screen, how nice!
import base64
encrypted="HEYGAwIKCxQSUlZbSUkAExAXFU5CR0YWGQ0FCwYGABNGSVRHRhAFFQwLCgQRUU1JSQIHExkTHR1AQU9WRgAABBMQEggLAgJGWVZGCA0PCBAABAQLCRVSVltJSRIPGRkCAgsDRllWRhsPBQMcAhJOTl1BUgUADwtATVVRBwYBQEFPVkYeBwlAUgs="
my_eyes=str.encode("gauvain")
decoded=base64.b64decode(encrypted)
decrypted=""
for i in range(0,len(decoded)):
decrypted+=chr((my_eyes[i%len(my_eyes)] ^ decoded[i]))
print(decrypted)➜ foobar python end.py
{'success' : 'great', 'colleague' : 'esteemed', 'efforts' : 'incredible', 'achievement' : 'unlocked', 'rabbits' : 'safe', 'foo' : 'win!'}
And thus Foobar concluded…or did it? Actually there’s a thing I haven’t told you and I spent most of my time on during Expanding nebula: remember when I told you I stopped using asserts at some points? Yeah no I’m not gaslighting you I actually wrote it between the lines of this incomprehensible tech mombo jumbo, well there was a simple reason for that:
When using asserts in Foobar in my answers questions, I right away saw that they removed the custom text you put there and only keep type and line of the exceptions, like this:
foobar:~/expanding_nebula gauvain$ verify solution.py
Verifying solution...
MemoryError [line 13]
But then later I misindented some of my foobar asserts, running in the global scope and I realized I somehow had the text printed this time…? At this point I decided to drop off the asserts and wait for the final challenge to have more time to understand if I could take advantage of that, and I did!
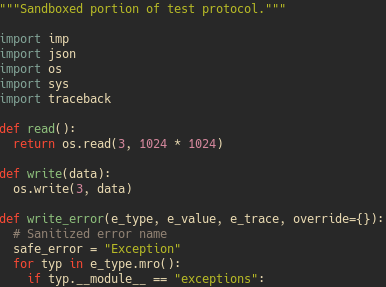
Oh, you're giving me your source code?
I had full read access to the VM. Time to dump everything!
It took me something like one hour of painfully editing dumping scripts
just to dump one file because of the 1mb memory limit, also had a limit on how
much files were opened and time limit so I had to edit by hand my dumping
scripts but eventually…
➜ ~ file ~/Documents/PROJECTS/PROGRAMMING/SOFTWARES/foobar/hack/dump/export/pypy/bin/pypy
/home/govanify/Documents/PROJECTS/PROGRAMMING/SOFTWARES/foobar/hack/dump/export/pypy/bin/pypy: ELF 64-bit LSB shared object, x86-64, version 1 (SYSV), dynamically linked, interpreter /lib64/ld-linux-x86-64.so.2, for GNU/Linux 2.6.26, BuildID[sha1]=a4cfb928b3d0a034b2b94b0c2b19b89ef75369cc, stripped
Woop, full dump! So now time to study foobar test VM: it contains 2 folders, /tmp and /pypy, with one file, /main.py, which executes our code. In a nutshell this one does read from the file descriptor 3 the source code, the function, try to locate if it exists and then execute it for each test case given by the file descriptor 3, writing each time the result to this mystery 3 again. From this point forward we have pretty much got code execution into Foobar but that is laaaame, the pypy binary is kinda old, 2016 to be exact, so let’s get some RCE, will we? To be honest though this was really unecessary as no real checks are in place to lock down our code, as the VM is ALREADY locked down: no network, time limited, read-only, not fun, and we could still interact with the file descriptor without getting an RCE to leak the test data. And that’s pretty much where I stand by now: the VM is locked down by nsjail through the intel I got, which while having a fairly small codebase(5k) it relies on concepts I am not super familiar with and core Linux namespaces, which seems pretty solid, so so far no dice for me, otherwise I’d have written a more clickbait article on “How I hacked google” and would be in a bunch of random hacking articles. I guess. Or I would’ve totally been forgotten and just have bragging rights nobody cares about, that works too. Either way I am dead set on getting a sandbox escape from nsjail one day, but I haven’t been able to do much so far, sorry to end on something so anti-climatic but hey, what did you expected? I’m still 19.
Conclusion
And we made it, gosh finally. I hope I haven’t skipped too much for your
understanding or that my regular writing style didn’t took too much of an hit
from that(don’t worry I’m still silly) but I had 9 challenges to talk about and
a hacking part…so I tried to condense a bit this article. Either way there
wasn’t a lot to talk about on how I figured out the problems, up to level 2(3
first challenges) it was basically “just code and think later”, level 3 was
“how good can you be at looking up stuff on the internet”, but level 4 and level
5 were more intricate. For example when first looking up the levl 4 stuff I had
written a test case of all the numbers that loops and tried to pair them in a
simple fashion in the best way possible, which ended up being lesser used node A
to lesser used node B.
So yeah, I had way too much things I wished to talk about but couldn’t, if you
wanted to know more about foobar aesthetics I guess you should look it up online
too, or just get this js and css and do a basic webpage from that ;)
The CSS
and the JS
They’re archived directly from the domain using the Web Archive, so it’s pretty
much guarenteed that I haven’t edited them myself.
There’s one thing I can say about foobar that I think is really neat though: I
finished the 9 challenges of foobar in less than 200 lines of code and I’m sure
I could’ve done better, so this seems pretty accurate of the code quality that
someone can produce(or if he just calculates a bunch of predefined answers like
I almost did for Expanding Nebula…seriously that thing was some hell).
Ah yeah for the people wanting to do Foobar without using Google or just
spamming ranodm keywords there(trust me I tried), there is more than one way to
get in. Seriously just keep looking, you’ll find a way through eventually.
Anyways I hoped you liked this article as much as I liked writing it, the challenge was really fun, albeit a bitoverhyped. I now have my second Google referral for a job to use whenever the hell I want though! But yeah, Google Foobar is really just a glorified month-spanning interview for Google, no new Cicada 3301 lying under the lines(I should actually look at the Liber Primus one day by the way, sounds like a fun way to waste time trying to decrypt garbage).
Meanwhile as promised my code is available in full there, if this wall of text actually inspired you or something.